Reduction
Accurate simulations, especially in the case of models involving strong coupling between multiples physical fields, require complex numerical models that reveal to be costly in terms of computation time.
The principle of model reduction methods consists of processing the complete numerical model to extract a reduced model that involves very few variables but remains representative of the initial model behavior of interest.
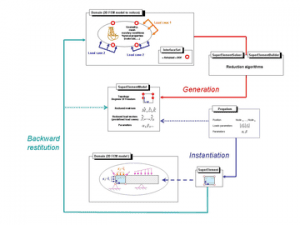
Model reduction flow
The reduced models can be simulated using dedicated software tools, such as OOFELIE::Multiphysics in MS Excel or they can also be included in a more complex finite element model as sub-structures.
The first step consists in the creation of the model to reduce. It corresponds usually to a standard finite element model that includes a mesh, the definition of the type and properties of finite elements, boundary conditions, and loads. The reduction does not involve any particular requirement. Nevertheless, the model must be consistent, that means well defined, and the physical behavior it addresses must match the scope of the available reduction algorithms.
In addition, the user selects “retained” degrees of freedom (DOF), which means that the DOF of interest in terms of which the model will be reduced. These DOFs are usually the DOF that characterize the behavior of the system and the DOFs that are used to connect it with its environment. According to the algorithm used to reduce the model, the user can also select additional variables to match his requirements in terms of reduced model accuracy. The application of the reduction algorithms implemented in OOFELIE::Multiphysics generates a model of superelement. This is a data structure that describes the reduced model topology and its internal definition in terms of DOF and equations governing its behavior.
The models of superelement are used to generate one or multiple superelements in a generic finite element model. Indeed, a superelement can be simulated independently or multiple superelements can be combined together if each of them corresponds to a substructure. The generation of a superelement is called “instantiation”. The simulations of superelements can be performed in OOFELIE::Multiphysics in MS Excel thanks to the interface that has been developed. Finally, the results computed using reduced models can be expanded to the initial model used to generate the superelement model. This last step is called “backward restitution”. This operation allows the visualization of the complete physical fields on the initial geometry. This can be particularly interesting as reduced model results involve only global variables.
Interfaces
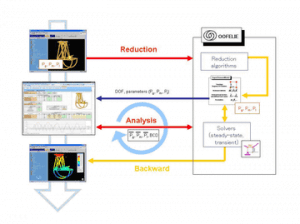
In order to provide user friendly interfaces, the model reduction feature has been integrated in OOFELIE::Multiphysics and in MS Excel as illustrated on the following picture.
At the top level, the user uses OOFELIE::Multiphysics to create his 3D model, to define reduction settings, and to perform the extraction of the reduced model. OOFELIE::Multiphysics applies the appropriate reduction algorithm to the model and generate a model of superelement. The super element model, which is parameterized, can be imported in MS Excel, thanks to a dedicated interfaced that has been developed. Using this MS Excel interface, illustrated in the following pictures, the user can easily define the boundary conditions and excitation to apply on the model and define the simulation settings.
Export to EDA
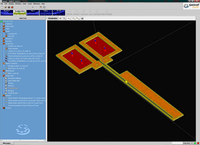
This feature is intensively used in the microsystems (MEMS) component design procedure. Indeed, simulations at the circuit level require accurate compact models of the MEMS components, also called behavioral models, macromodels, or reduced-order models (ROM), to be generated from a 3D expensive numerical model. These reduced models are written in HDL (Hardware Definition Language) and inserted, in a schematic form, is specific microelectronic simulators.
OOFELIE::Multiphysics comes with capabilities to generate reduced order model from full 3D numerical simulation and export them in VHDL-AMS or Verilog-A format for co-simulation in EDA simulators (for e.g. TANNER EDA from Mentor Graphics)
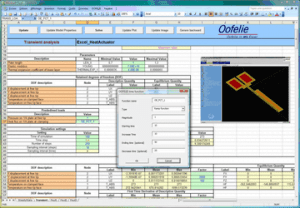
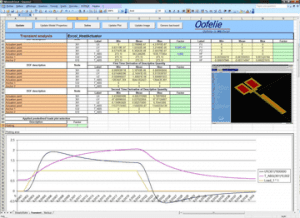
The following pictures compare the results of simulations obtained using a 3D model and a reduced model of a heat actuator MEMS. It can be seen that the accuracy of reduced models is fully compatible with industrial applications.
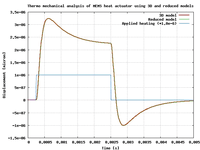
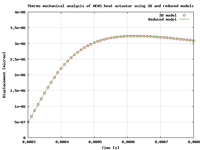
The reduced models can also be introduced in simulation of systems involving control loop in order to perform fast simulation of the whole system behaviour.
In a similar way, the introduction of reduced models in optimisation procedure can be very efficient and can reduce significantly the time of simulation required to reach convergence.